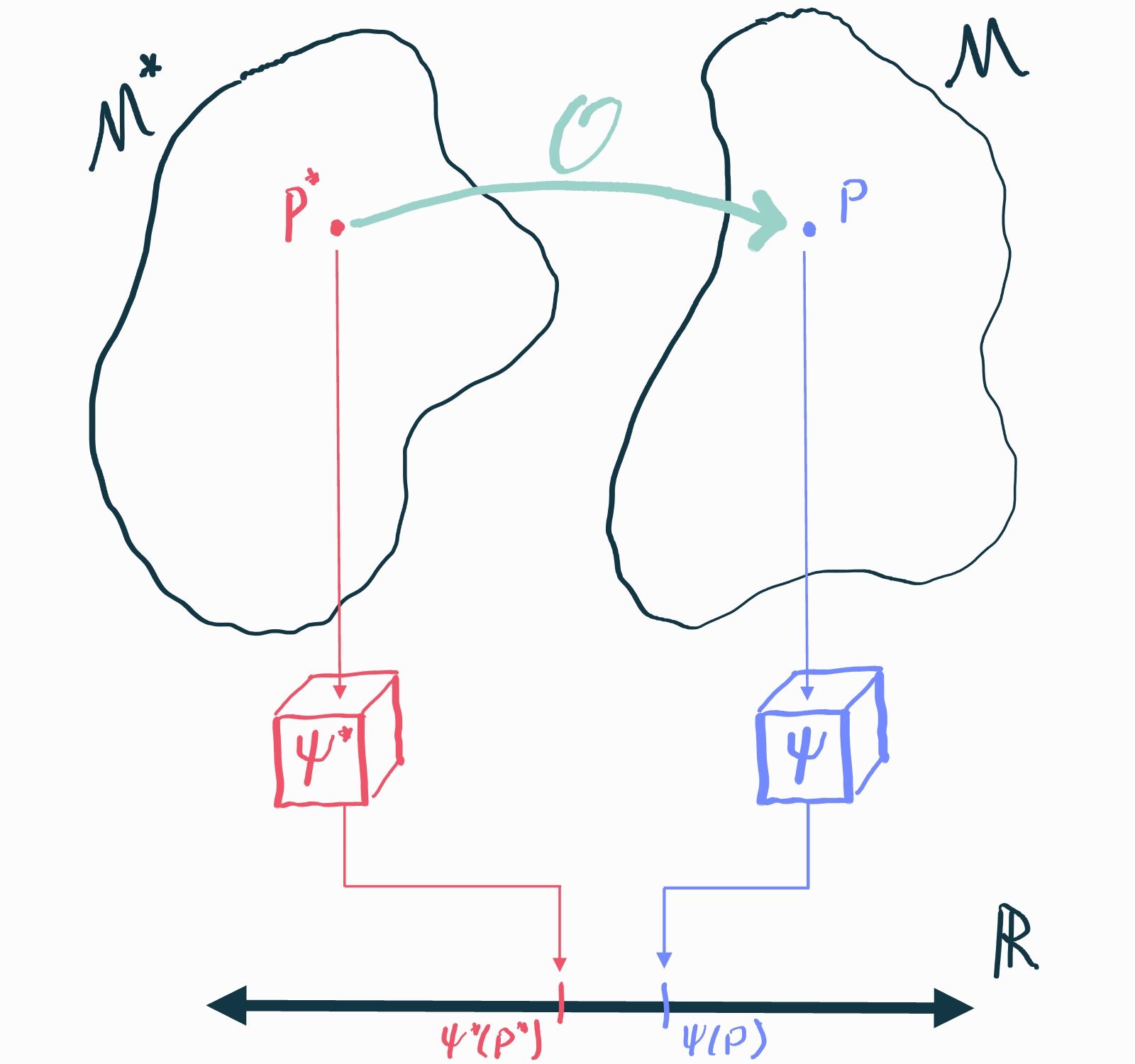
Now that we've understood the basics of inference, we can introduce causality. Causal inference questions are just statistical inference questions but in an imaginary world where we can always observe the result of alternative "what if"s. Yes, that's right, now there are two imaginary worlds: one which describes the distribution of the observed data (the statistical model we've been working with) and one which describes the distribution of all of the what-ifs (the causal model). For inference to be "causal" we need a way to link these two imaginary worlds together to guarantee that the answer to a statistical inference problem in the statistical world actually represents the answer to our causal question in the world of "what if"s. That will usually require making some assumptions about the causal model (e.g. presuming we've measured every covariate that could impact both treatment and outcome in either treatment arm).
This process, which is called causal identification, doesn't require any data and has nothing at all to do with statistical inference. That's why there is really no such thing as a "method for causal inference": once we've decided on the assumptions we need to establish identification, the "causal" part is completely done and the rest is just vanilla inference as we described it in the last chapter.
Understanding identification will also help you see why a well-defined intervention is important to formulating something as a causal question. It is also key to understanding methods that quantify the impact of potentially erroneous identifying assumptions.
Credit Due
Once again I owe most of my understanding of these ideas to the Statistical Roadmap of Petersen and van der Laan as well as to didactic introductions by Edward Kennedy. Potential outcomes are usually attributed to Jerzy Neyman and Donald Rubin. Judea Pearl is a titan in the world of identification whose contributions over the past decades cannot be understated (e.g. nonparametric structural causal models). I owe a lot of my understanding of identification strategies to various papers by Eric Tchetgen Tchetgen. For partial identification, the canonical reference is Manski, although some ideas date back to Jerome Cornfield. Papers by Tyler VanderWeele and Peng Ding have helped me understand the principles of sensitivity analyses; Ivan Diaz and Mark van der Laan first introduced general-purpose sensitivity analyses based on the causal gap.