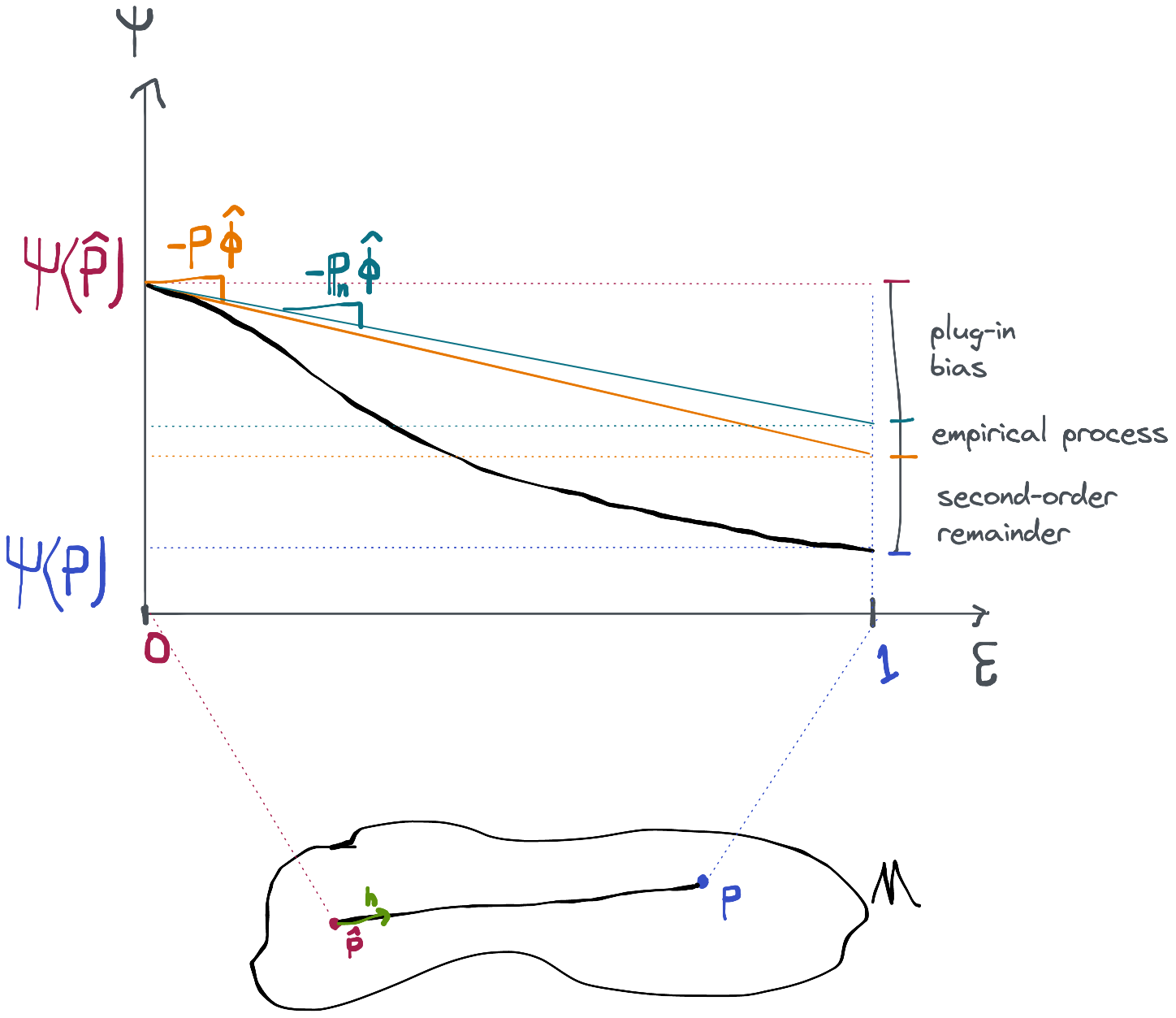
What we showed in the last section was how to identify the efficient influence function for a particular model and parameter. If we know the EIF, we know that any estimator that can be proven to have this as its influence function will attain the smallest possible asymptotic variance among RAL estimators. That should let us verify that an estimator is efficient, but it doesn't tell us how build such an estimator from scratch.

It turns out that there are three different strategies that accomplish this goal: bias correction, estimating equations, and targeted estimation (TMLE). It's important to understand that these are strategies for building an efficient estimator. Without prior reference to a specific estimation problem (model and parameter), it's not appropriate to refer to, for example, "the estimating equations" estimator or "the TMLE". There are many TMLEs, one for each estimation problem. Moreover each of these strategies can have small variants, e.g. weight-stabilized estimating equations or C-TMLE, which further distinguish them from the top-level strategy.

It's natural to ask: if these three strategies (and all their minor variations) accomplish the same goal of building an efficient estimator, what's really the difference? The answer is somewhat subtle. Yes, all three strategies give you an efficient estimator at the end of the day, but the way we've defined it, efficiency is an asymptotic property. The estimators you get out of these three strategies will all behave the same in large-enough samples, but in smaller samples they might behave very differently! Moreover, although all three produce efficient estimators under the same set of assumptions, we might also be interested in how the results differ between the three when some of those assumptions are not met (though this is of less importance today than it was historically). These considerations motivated the historical development first of estimating equations out of the bias-corrected approach, and then later of TMLE out of the estimating equations approach. TMLE is the most modern, elegant, and robust approach so far.

Before we get into any of that we'll start with a simpler approach that we'll call a naive plug-in estimator. An analysis of this kind of estimator will reveal exactly what conditions need to be met to construct an estimator that has the efficient influence function. We will see that these conditions are extremely mild and/or that we can provably satisfy them in practice. We'll conclude that we can build efficient estimators for most statistical estimation problems without making any scientifically meaningful statistical assumptions. Once we have those conditions in place, we'll return to bias correction, estimating equations, and TMLE and show how they each satisfy them in their own way.

At the end of the chapter we'll discuss how to do valid inference (e.g. build confidence intervals and p-values) for any of these efficient estimators in a very simple way.

(Nonparametric) efficient estimators first appeared in the 70’s with the work of Pfanzagl and others but the first comprehensive treatment that I know of is the text by Peter Bickel et al. Development of the later estimating equations methods was spearheaded by Jamie Robins and associates (e.g. Andrea Rotnitzky). The seminal text on those methods is van der Laan and Robins. Targeted maximum likelihood was then developed by Mark van der Laan and others, with van der Laan and Rose serving as the comprehensive reference. The development of the universally least-favorable path is due to van der Laan and Gruber, while the highly adaptive lasso is due to Benkeser and van der Laan. My own comprehension of the general asymptotic analysis of these estimators is due largely to tutorials by Edward Kennedy, lectures by Mark van der Laan, and the basics of empirical process theory found in van der Vaart 1998.