In this chapter we discuss the fundamental goal of statistics: to infer some hidden property of the real world (and some notion of our certainty about it) just by observing a finite number of experimental measurements. To do this without shooting ourselves in the foot, we need to clearly define what it is we're trying to figure out about the real world before we go mucking around with data. We need to be explicit about what we are assuming about the world that generated our data.
Not defining a clear question or set of assumptions is by far the largest source of catastrophic errors in any data analysis. Why? Because no matter what you do with the data, if you didn't have a clear question to begin with, whatever answer you've arrived at is completely meaningless. You'll often see analyses that start with "we took the data and did linear regression; here we report the coefficients and confidence intervals". Without specifying a concrete goal, how can we judge what these coefficients are supposed to mean? Without a clear description of modeling assumptions, how can we know that the confidence intervals actually have their promised level of coverage? You could have infinite data and still get it all wrong: don't forget that data science is about science and not just data. Leaving questions and assumptions implicit causes confusion.
It's not always easy to pin down a good question. Most of the time, domain experts actually have a large swath of vague, interlocking questions: it's part of the statistician's job to wrangle these down to something concrete. Moreover, it's understandable that many statisticians and data scientists struggle to clarify their analyses.
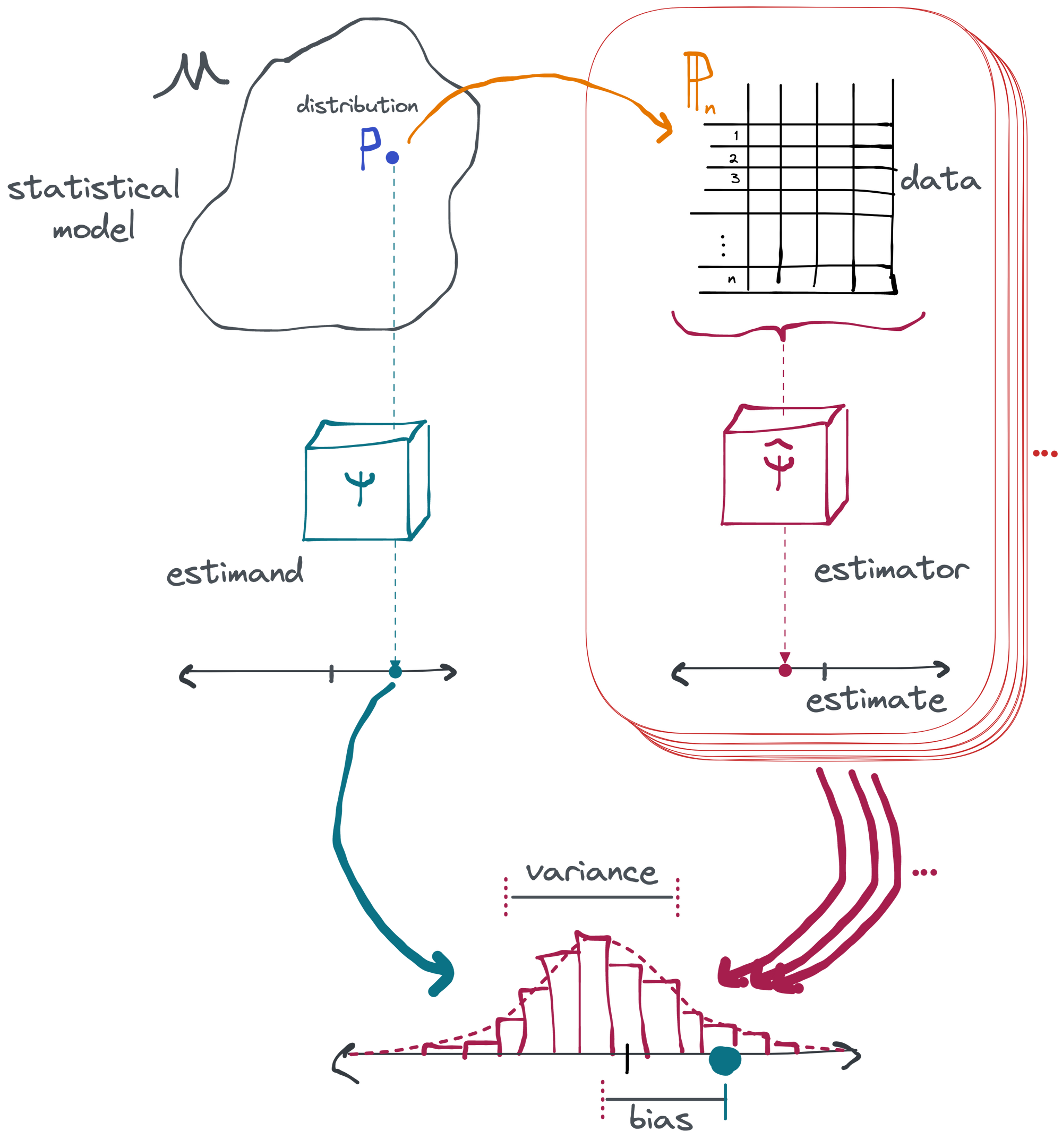
When we talk about defining a question (and assumptions) what we mean concretely is having a clear, unambiguous picture in your head about the kinds of mathematical processes that could have generated the data and what attribute or characteristic of the data-generating process you are interested in. This is by necessity an abstract and imaginative process: you can never point to a physical "data-generating distribution" that exists in the real world. These constructs really only exist in the mind of the statistician, but they cannot be done without if you want to meaningfully interpret the result of an analysis.
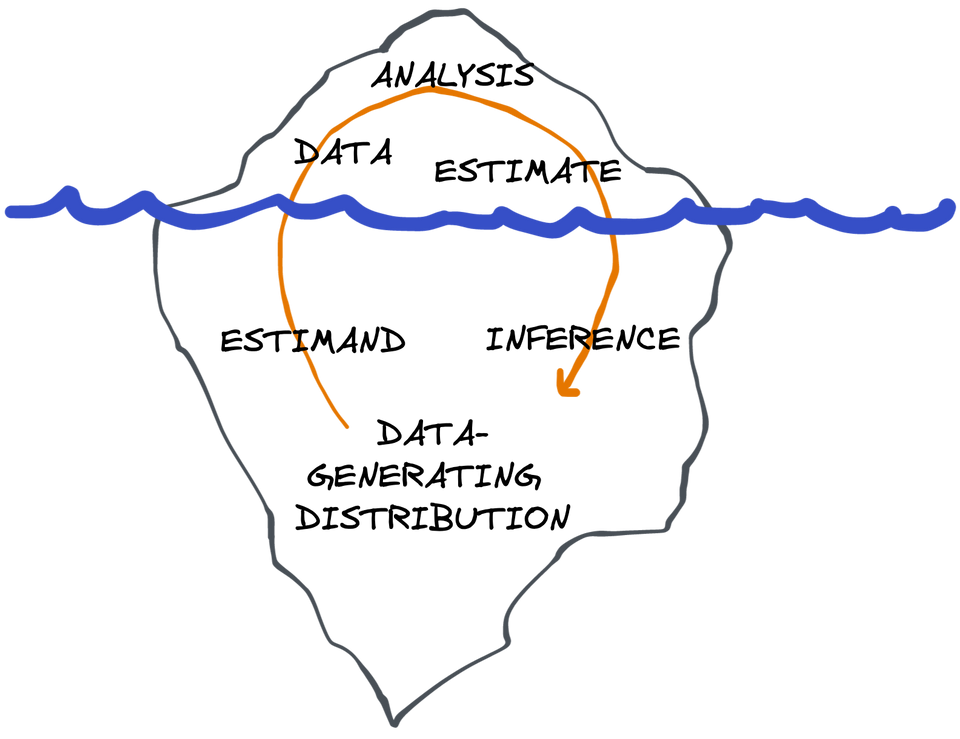
You can think of this as an iceberg: you get to see the data, what you do with it, and the results. These are all things you can see and "touch" (at least in a computer program). But that's only the tip of the iceberg, the 10% above the waterline. Under the surface, you have an imagined space of data-generating distributions (different plausible versions of "the real world"), functions that act on these distributions to reveal their true properties (i.e. definitions of "the answer" in each "world"), and an infinite number of repetitions of the statistical processes that generated the data (to allow for a quantification of uncertainty). That's the 90% of the iceberg that remains submerged; imaginary. Outside of simulations, you can't ever touch these things. It's your job to know they are there. The tip of the iceberg can't exist (or at least doesn't mean anything useful) without the hidden mass below.
First, you must define the question and your assumptions and formalize them mathematically. Only then should you start looking at your data and think about what you're going to do with it.
To make all these concepts concrete we'll start by going through the components of a descriptive analysis (the "tip of the iceberg") before adding the components that are necessary for inferential analyses (what's "below the surface").
Credit Due
This way of thinking about statistics has been around implicitly for a long time, albeit couched in a parametric setting. Although many people have contributed to liberating it from parametric assumptions, including Jamie Robins and Anastasios Tsiatis, the clearest nonparametric exposition is given by the Statistical Roadmap envisioned by Maya Petersen and Mark van der Laan (and popularized to a great extent by Laura Balzer, Sherri Rose, and others). I (Alejandro) myself first encountered a clear articulation of this perspective in the work of Edward Kennedy, which was reinforced by Peter Aronow and Benjamin Miller. To my knowledge, Judea Pearl gave the first cohesive account of nonparametric structural causal models. I also owe credit to Jeff Leek and Roger Peng for clarifying differences between various kinds of scientific questions. Miguel Hernan has several papers that helped me understand the best practices for turning scientific questions into mathematical abstractions.